Sukses Ujian Nasional (Un) 2018 # Lingkaran, Sudut Sentra Dan Sudut Keliling.
 mie-indonesia.com ☺ Sukses Ujian Nasional (UN) Sekolah Menengah Pertama 2018 # Lingkaran, sudut sentra dan sudut keliling. selanjutnya ........ atau lihat dulu @Daftar Isi.
mie-indonesia.com ☺ Sukses Ujian Nasional (UN) Sekolah Menengah Pertama 2018 # Lingkaran, sudut sentra dan sudut keliling. selanjutnya ........ atau lihat dulu @Daftar Isi. Lingkaran merupakan salah satu bentuk bangkit datar yang unik sehingga banyak benda-benda yang yang dibuat dengan rujukan lingkaran. Mengapa unik ? Keunikan salah satunya ialah apabila dibuat menjadi bentuk bangkit ruang sanggup menggelinding tepat di permukaan datar serta seluruh permukaan tepinya sama.
Keunikan bentuk lingkaran ini dalam benda-benda bangkit ruang yang dikenal dengan bentuk lingkaran contohnya dipraktikan pada pembuatan ban, bola, piring, uang koin dan lain-lain. Karena keunikannya, dalam ilmu matematika lingkaran ini juga memakai konstanta khusus untuk menghitung keliling dan luasnya yang dikenal dengan nama phi.
1) Unsur-Unsur Lingkaran
Perhatikan gambar berikut ini.
a. Jari-jari : Jarak dari sentra lingkaran (P) ke titik pada lingkaran. PA, PB, PC, dan PD merupakan jari-jari lingkaran P.
b. Tali busur (garis warna biru) : ruas garis yang menghubungkan dua titik pada lingkaran. AB merupakan tali busur lingkaran P.
c. Diameter : tali busur yang melalui sentra lingkaran. BD merupakan diameter dari tali busur terpanjang pada lingkaran P.
d. Apotema (garis warna merah) : jarak tali busur ke sentra lingkaran. PE merupakan apotema tali busur AB pada lingkaran P.
e. Busur (garis lengkung hijau) : garis lengkung yang menghubungkan dua titik pada lingkaran. Busur merupakan bab dari keliling lingkaran, lihat titik F. Garis lengkung AB merupakan busur lingkaran P.
f. Juring (daerah warna abu-abu) : kawasan yang dibatasi oleh dua jari-jari dan sebuah busur. Juring merupakan bab dari luas lingkaran. Daerah PCD merupakan juring lingkaran P.
g. Tembereng (daerah warna pink) : kawasan yang dibatasi oleh sebuah tali busur dan busur lingkaran. Daerah AFB merupakan sebuah tembereng.
2) Keliling dan Luas Lingkaran
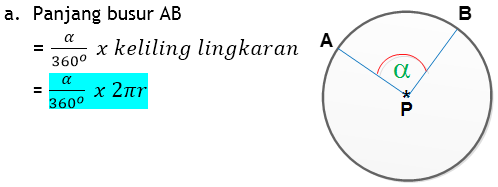
3) Panjang Busur dan Luas Juring
4) Luas Tembereng
5) Hubungan Sudut Pusat, Panjang Busur dan Luas Juring
6) Sudut-Sudut pada Lingkaran dan Hubungannya
7) Hubungan Dua Lingkaran
8) Sifat Segi Empat Tali Busur
9) Sudut Antara Dua Tali Busur
10) Garis Singgung Lingkaran
a. Sifat-sifat garis singgung lingkaran
1) memotong lingkaran di satu titik.
2) tegak lurus dengan jari-jari yang melalui titik singgung.
b. Panjang garis singgung lingkaran
1) Garis singgung melalui satu titik di luar lingkaran.
2) Garis singgung komplotan luar
3) Garis singgung komplotan dalam
Contoh Soal
1) Perhatikan gambar berikut ini.
Jawab :
2) Perhatikan gambar berikut ini.
Jawab :
Lihat rumus point 5) di atas.
3) Perhatikan gambar berikut ini.
Jawab :
Soal-Soal Latihan
1) Diketahui dua lingkaran dengan jari-jari 2 cm dan 6 cm. Jika jarak titik sentra kedua lingkaran tersebut 17 cm, berapakah panjang garis singgung komplotan dalamnya ?
2) Dua lingkaran berpusat di A dan B dengan jarak AB = 20 cm. Panjang garis singgung komplotan dalam 16 cm dan panjang jari-jari lingkaran dengan sentra A = 5 cm. Berapakah panjang jari-jari lingkaran yang berpusat di B ?
3) Perhatikan gambar berikut ini. (hal 62 no 27)
Setelah mempelajari teori di atas, pembahasan tiga soal di atas dalam video yang sanggup disaksikan berikut ini, atau klik YOUTUBE disini
Terima kasih kepada siapa saja yang telah melihat, membaca, men-share atau men-follow artikel ini.
☺☺Motivasi, Inspirasi dan Edukasi Indonesia☺☺























Komentar
Posting Komentar